Übung 6

Sampling Design

R eignet sich hervorragend um ein Sampling Design umzusetzen. Am ersten Tag des CAS habt ihr etwas zu Sampling Design gelernt (siehe Abbildung 6.2).

Folie Sampling Design

Abbildung 6.1



Schauen wir uns folgende Sampling Strategien an:

• zufällig
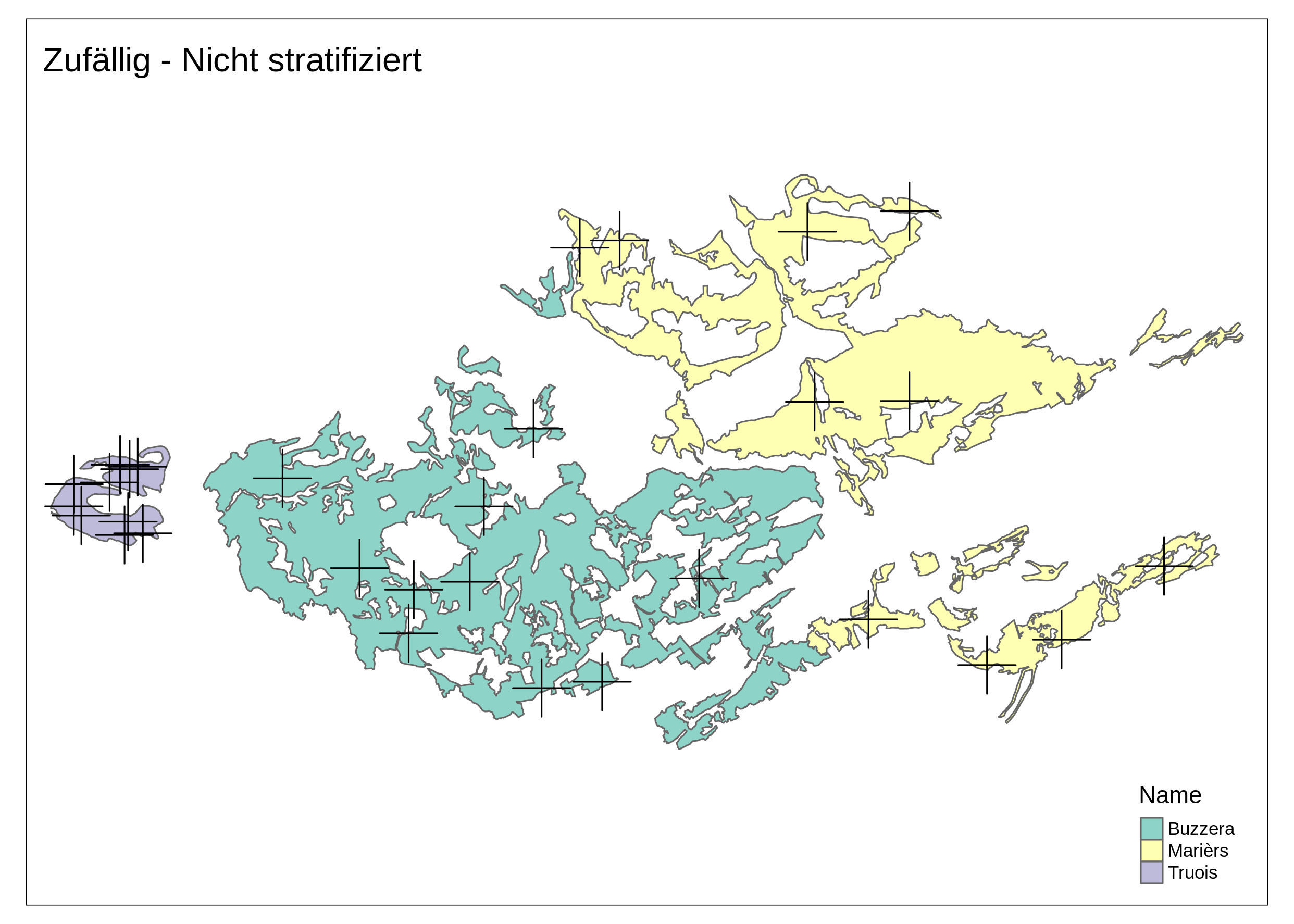
  • nicht stratifiziert (siehe Abbildung 6.2 (a) und Zufällig - Nicht stratifiziert)
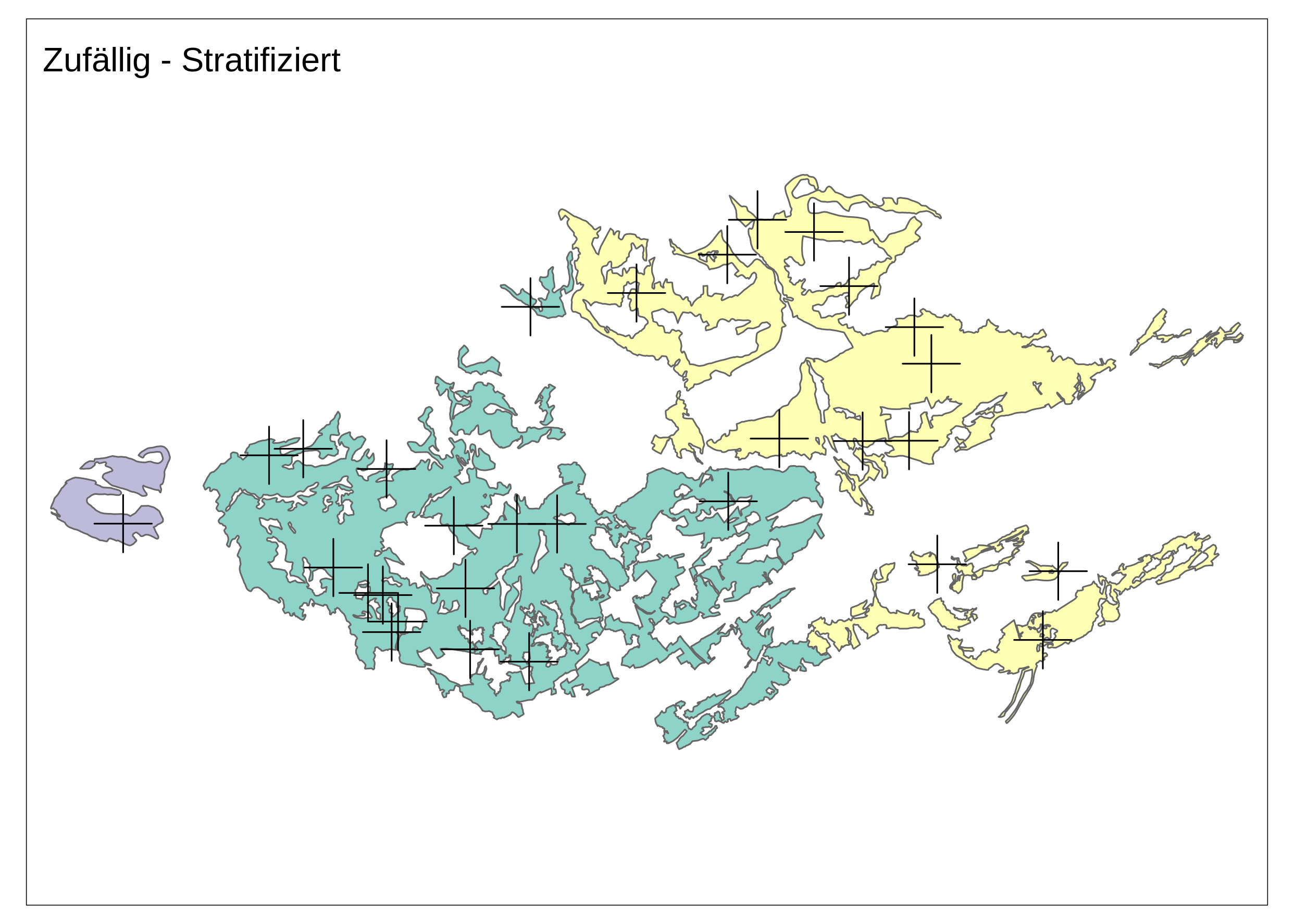
  • stratifiziert (siehe Abbildung 6.2 (b) und Zufällig - Stratifiziert)
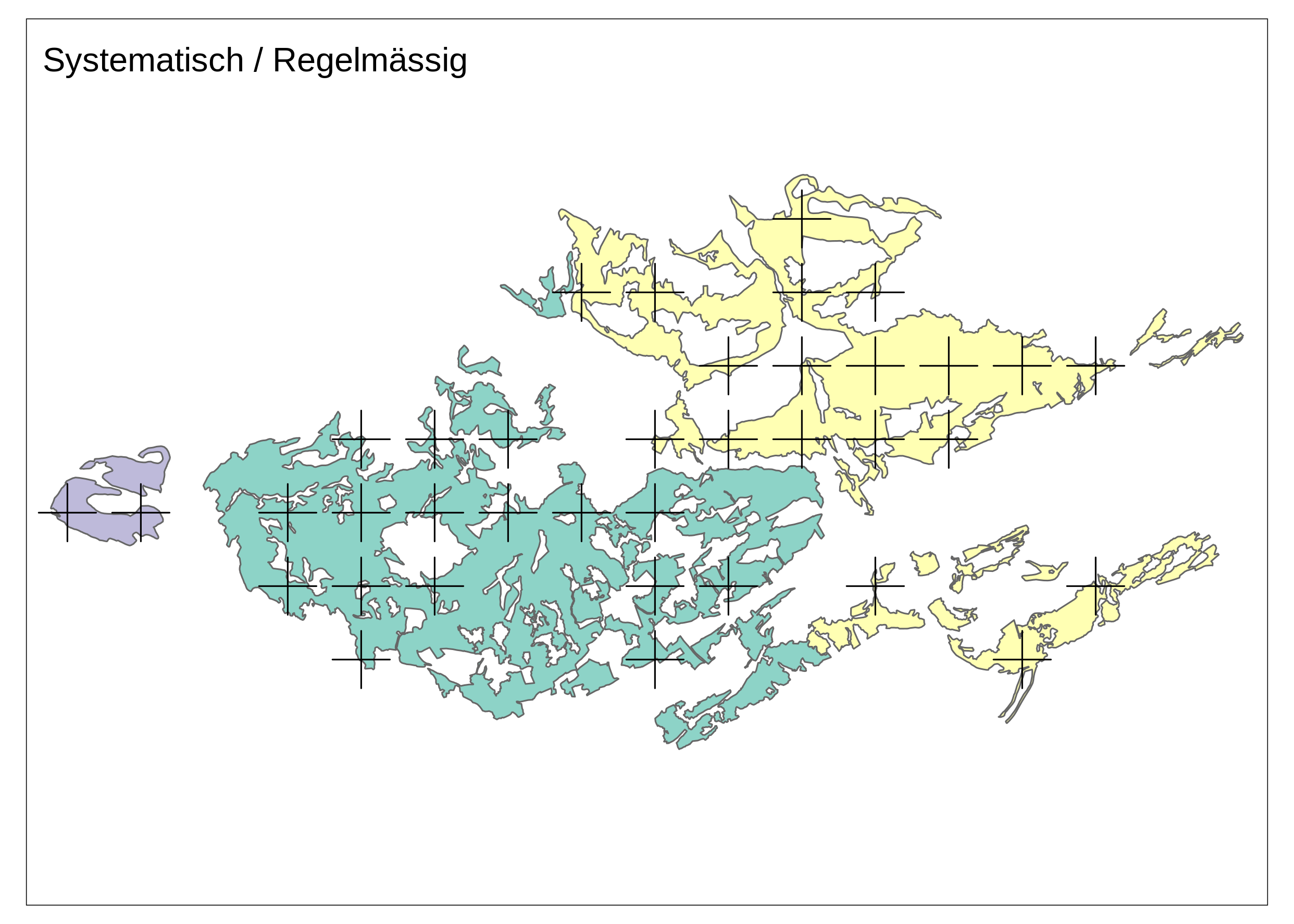
• systematisch / regelmässig (siehe Abbildung 6.2 (c) und Systematisch / Regelmässig)

(a) 30 Samples total, 10 Samples pro Lokalität

(b) 30 Samples total, verteilt nach Hektaren

(c) 30 Samples total, systematisch / regelmässig verteilt

Abbildung 6.2: Drei verschiedene Sampling Strategien

Vorbereitung

library("sf")
library("terra")
library("tmap")
tmap_mode("plot")

set.seed(1920)

tww <- read_sf("data-original/TWW/TWW_LV95/trockenwiesenweiden.shp")

1filter <- c("Marièrs", "Buzzera", "Truois")
tww <- tww[tww$Name %in% filter,]

2tww <- tww[, "Name"]

3tww$area_ha <- as.numeric(st_area(tww))/10000

4samples_total <- 30


5base_plot <- tm_shape(tww) +
  tm_polygons(col = "Name") +
  tm_layout(legend.show = FALSE, asp = 7/5)

1

Nur 3 Lokaliäten auswählen

2

Nur die Spalte “Name” (=Lokalität) behalten. Die Geometrie Spalte kommt automatisch mit.

3

Fläche berechnen und in Hektaren umrechnen (als Vorbereitung für die das stratifizierte Sampling)

4

Variabel erstelen für die Summe an Samples, die wir machen können / wollen

5

Optional: Da wir immer wieder die gleiche Karte machen, können wir eine Basis Karte erstellen und immer wieder benutzen.

Zufällige Verteilung

Für die zufällige Verteilung der 30 Samples, gibt es zwei Möglichkeiten: (1) Nicht stratifiziert und (2) Stratifiziert. In jedem Fall brauchen wir eine Spalte mit der Anzahl der Samples für die jeweilige Lokalität:

1tww$nicht_stratifiziert <- samples_total/nrow(tww)

2tww$stratifiziert <- round(samples_total/sum(tww$area_ha)*tww$area_ha)

1

Nicht stratifiziert: In jeder Lokalität gleich viele Samples (\(\frac{30}{3}= 10\))

2

Stratifiziert: Samples in Relation zur Fläche (\(A\)) verteilen (\(\frac{30}{\sum \text{A}} \times \text{A}\))

knitr::kable(tww)

Name	geometry	area_ha	nicht_stratifiziert	stratifiziert
Marièrs	MULTIPOLYGON (((2822107 119…	240.5064	10	13
Buzzera	MULTIPOLYGON (((2820384 118…	305.1896	10	16
Truois	MULTIPOLYGON (((2815810 118…	20.1714	10	1

Zufällig - Nicht stratifiziert

sample_plots1 <- st_sample(tww, size = tww$nicht_stratifiziert)

nicht_stratifiziert_plot <- base_plot +
  tm_shape(sample_plots1) +
  tm_dots(shape = 3, size = 3) +
  tm_layout(title = "Zufällig - Nicht stratifiziert", legend.show = TRUE)

nicht_stratifiziert_plot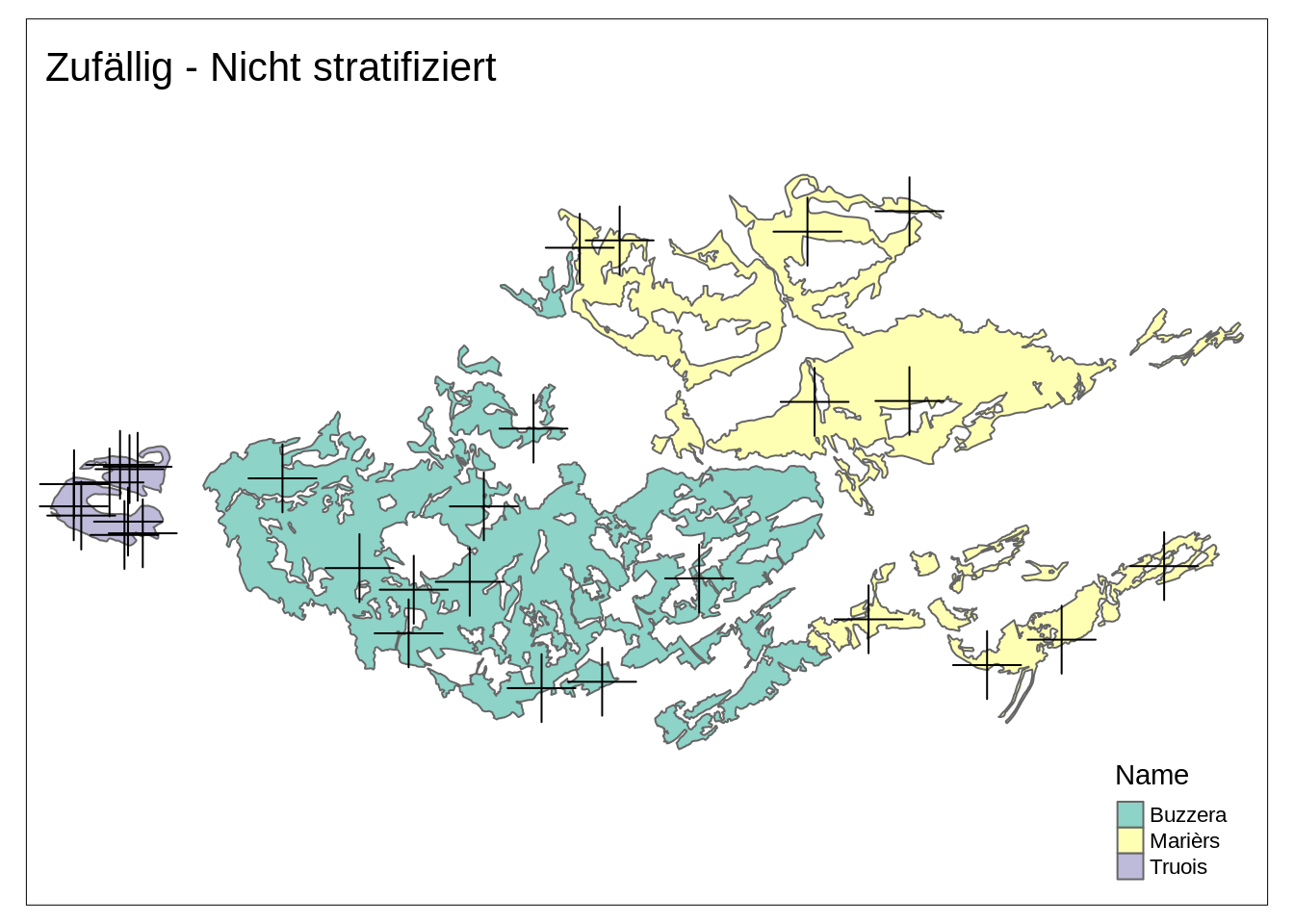

Abbildung 6.3

Zufällig - Stratifiziert

sample_plots2 <- st_sample(tww, size = tww$stratifiziert)

stratifiziert_plot <- base_plot +
  tm_shape(sample_plots2) +
  tm_dots(shape = 3, size = 3) +
  tm_layout(title = "Zufällig - Stratifiziert")

stratifiziert_plot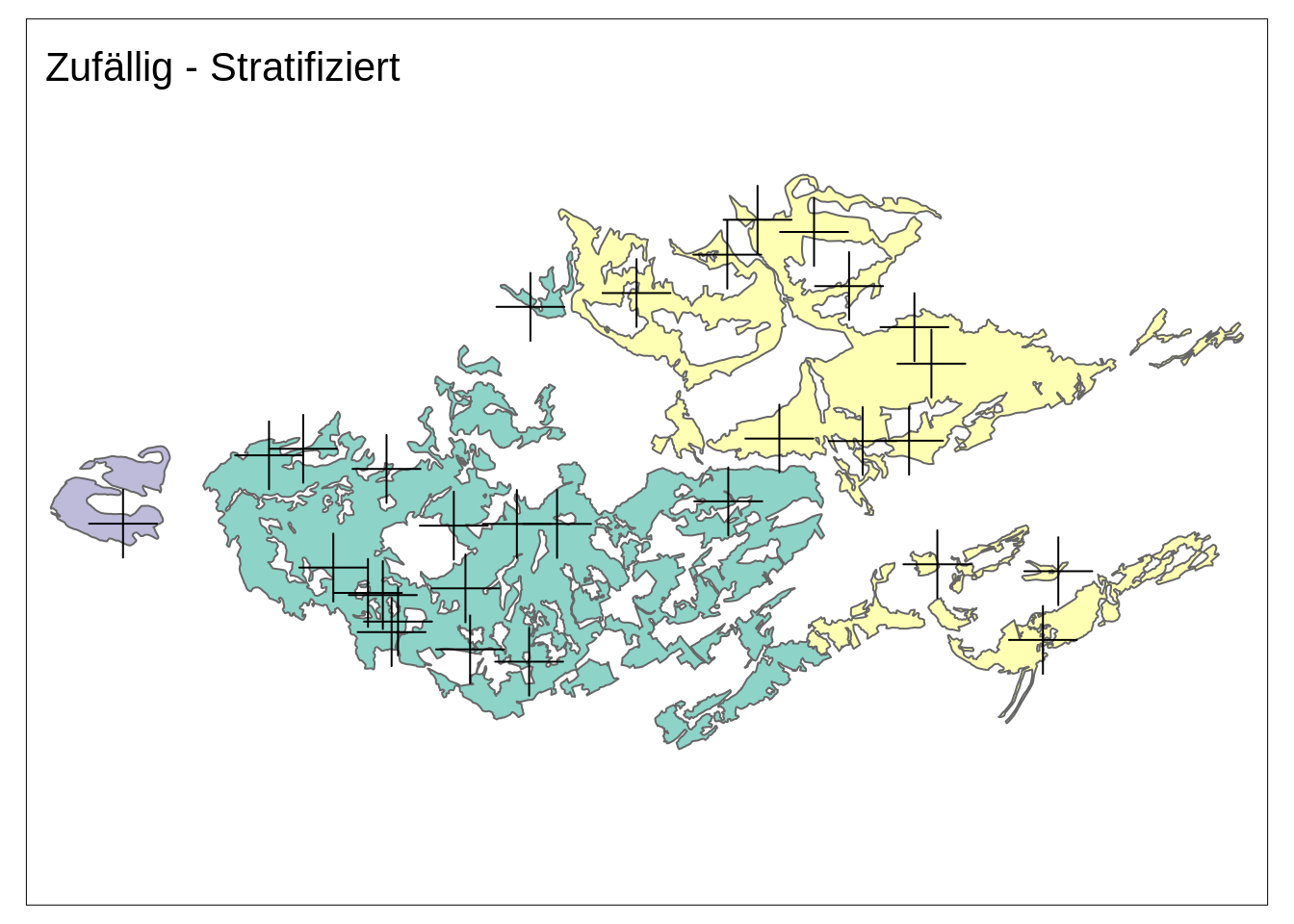

Abbildung 6.4

Systematisch / Regelmässig

sample_plots3 <- st_sample(tww, size = samples_total, type = "regular")

systematisch_plot <- base_plot +
  tm_shape(sample_plots3) +
  tm_dots(shape = 3, size = 3) +
  tm_layout(title = "Systematisch / Regelmässig")

systematisch_plot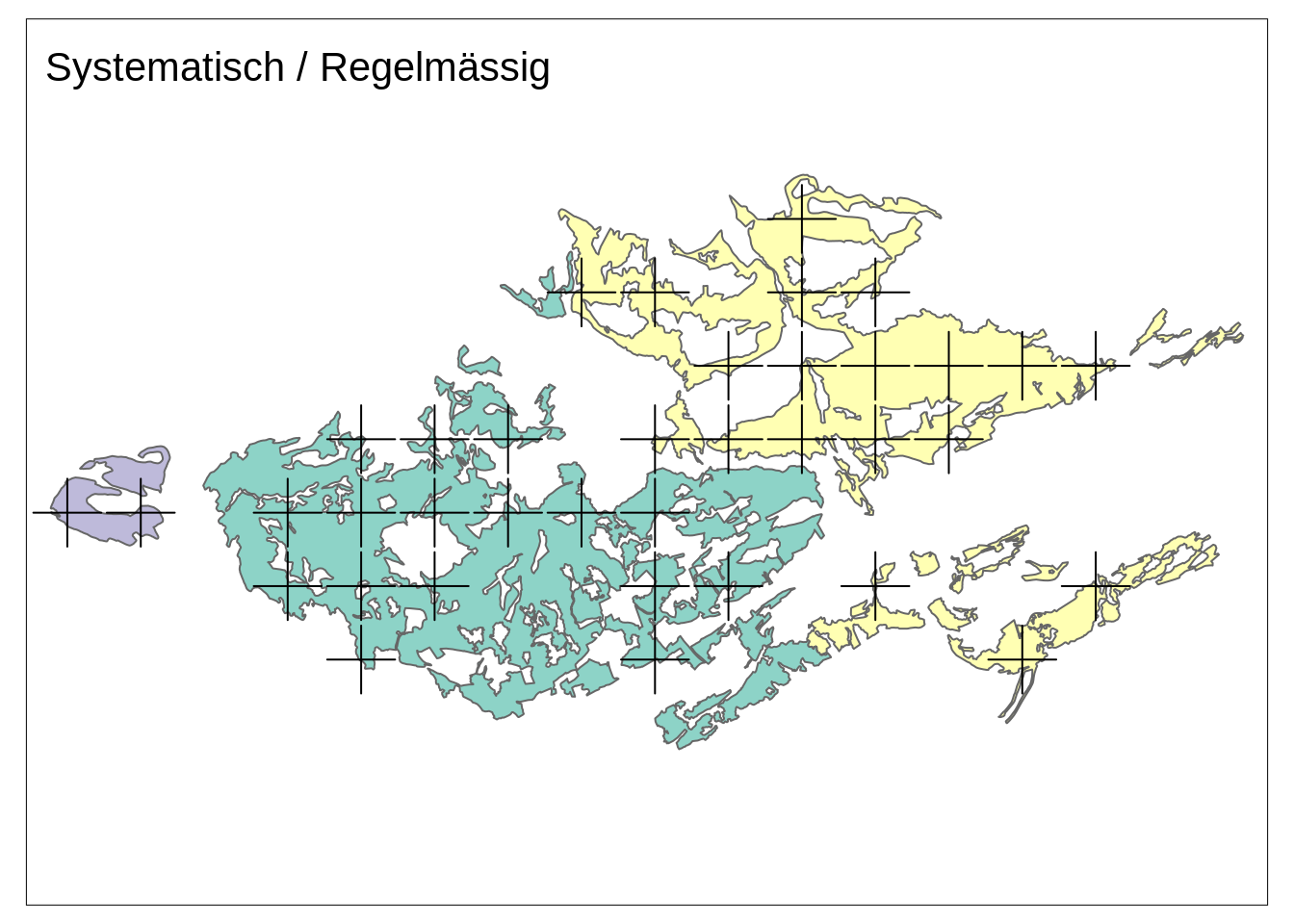

Abbildung 6.5

Übung

(Open End und ohne Musterlösung)

• Wähle einen kleineren Kanton oder eine Gemeinde aus
• Selektiere die TWW Standorte dieser Gemeinde / dieses Kantons
• Wähle ein sinnvolles Sampling Design und setze es mit R um
• Extrahiere die Höhenwerte für jeden Sample
• Visualisere in einer Karte:
  • die TWW Flächen
  • Gemeinde- / Kantonsgrenze
  • Sampling Standorte
  • Swissimage Hintergrund Karte
  • Nordpfeil, Scalebar